Question: What does a negative do to a graph?
Answer: Multiplying a function by a negative sign creates a reflection:
y = –f(x) or y = f(–x)
PUSHING THE Y-REFLECTION BUTTON
FLIPS FUNCTIONS ABOUT THE X-AXIS
y = –f(x)
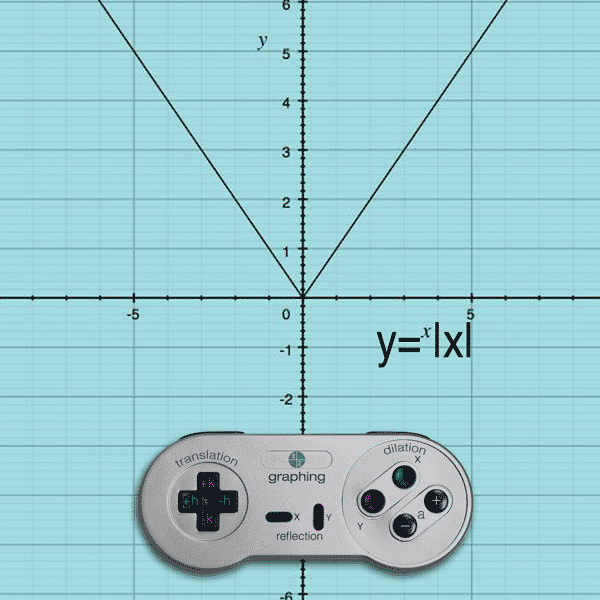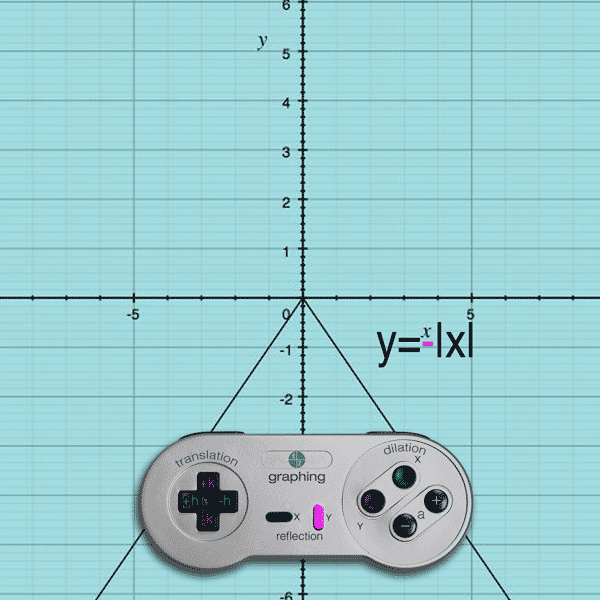
Do you see how the negative sign is on the outside of the function… affecting the y-value of the function? When you apply a negative to each y-coordinate of each point (x,-y), the graph flips across the x-axis.
Example: y = –|x| will flip the function about the x-axis
If the negative sign belongs to the y-value
the graph will reflect about the x-axis.
PUSHING THE X-REFLECTION BUTTON
FLIPS FUNCTIONS ABOUT THE Y-AXIS
y = f(–x)
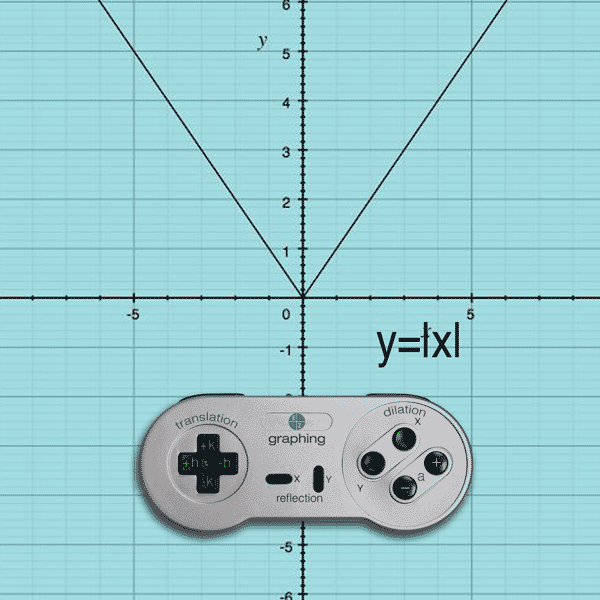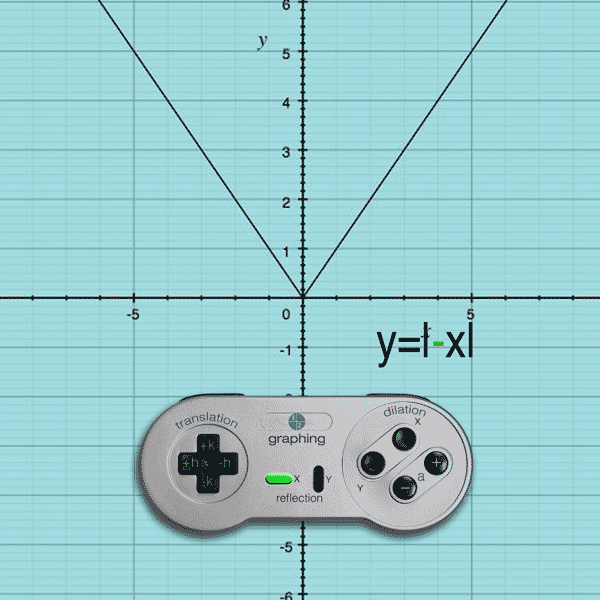
Do you see how the negative sign is on the inside of the function… affecting the x-value of the function? When you apply a negative to each x-coordinate of each point (-x,y), the graph flips across the y-axis. In this example, flipping the original function across the y-axis is identical to the original graph (so it looks like nothing happened).
Example: y = |–x| will flip the function about the y-axis
If the negative sign belongs to the x-value
the graph will reflect about the y-axis.
Remember Reflections: They appear like opposites
If the negative sign belongs to the y, then the graph will flip about the x-axis.
If the negative sign belongs to the x, then the graph will flip about the y-axis.